source: https://leetcode.com/problems/is-graph-bipartite/description/
Is Graph Bipartite?
There is an undirected graph with n nodes, where each node is numbered between 0 and n – 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v.
The graph has the following properties:
- There are no self-edges (graph[u] does not contain u).
- There are no parallel edges (graph[u] does not contain – duplicate values).
- If v is in graph[u], then u is in graph[v] (the graph is undirected).
- The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.
- A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
Example 1:
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
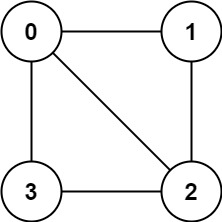
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
- graph.length == n
- 1 <= n <= 100
- 0 <= graph[u].length < n
- 0 <= graph[u][i] <= n – 1
- graph[u] does not contain u.
- All the values of graph[u] are unique.
- If graph[u] contains v, then graph[v] contains u.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
class Solution { public boolean isBipartite(int[][] graph) { int[] color = new int[graph.length]; for(int i =0;i<graph.length;i++) { if(color[i] == 0 && graph[i].length != 0) { if(!bfs(graph, i, color, 1)) { return false; } } } return true; } private boolean bfs(int[][] graph, int i, int[] color, int curCol) { color[i] = curCol; Queue<Integer> cur = new LinkedList<>(); cur.add(i); while(!cur.isEmpty()){ int size = cur.size(); for(int s = 0;s<size;s++) { int n = cur.poll(); for(int neighbor:graph[n]) { if(color[neighbor] == color[n]) return false; if(color[neighbor] == 0) { color[neighbor] = color[n] == 1 ? 2 : 1; cur.add(neighbor); } } } } return true; } } |